Robotika.cz » Guide » Řízení pohybu

Řízení pohybu

Author: Zbyněk Winkler, 2007-12-05

a co je to vlastně ta zpětná vazba

Máme k dispozici informaci z enkodéru zabudovaného do serva, kterému umíme generovat řídící signál. Nyní si vysvětlíme, jak tyto informace využít k jeho řízení. Zajímat se budeme zejména o servo modifikované pro kontinuální otáčení. Popsaný způsob je ale možné aplikovat i pro řízení obyčejného motoru s enkodérem, jaký se hodí pro použití i ve větším robotovi.

Máme k dispozici našeho servobota a jedním z cílů, kterých bychom chtěli dosáhnout, je i jízda rovně vpřed. Přestože se na první pohled může zdát že jde o triviální úlohu, spíše opak je pravdou. Sám od sebe totiž prostě rovně nepojede . Jedním z nešvarů elektromotorů je, že se typicky točí na jednu stranu rychleji než na druhou. Pro diferenciálně řízeného robota to ovšem znamená, že i při plném výkonu obou motorů má tendenci zatáčet — často i nepravidelně. Navíc se čas od času některý z motorů zadrhne nebo některé kolečko najede na nějakou nerovnost a podobně.

Shrňme si naši výchozí situaci:

umíme měnit šířku řídícího pulzu serva od 0.5 do 2.5 ms
enkodéry nám vrací počet ujetých tiků

Šířka pulzu 0.5 ms odpovídá maximální rychlosti na jednu stranu, šírka 2.5 ms pak maximální rychlosti na stranu druhou. Rychlost spočítáme z počtu ujetých tiků za daný čas.

Řízení bez zpětné vazby

První pokus o řízení rychlosti by mohl vypadat například takto:

pulse_width = (min_width + max_width)/2 + (req_speed/max_speed)

Výpočtem pro požadovanou rychlost req_speed určíme šířku pulzu na základě informace o rychlosti maximální. Za zmínku určitě stojí fakt, že tento přístup nevyužívá informaci o aktuální rychlosti a teoreticky by ke své funkci ani nepotřeboval enkodér. Skutečnost je však „maličko” složitější .

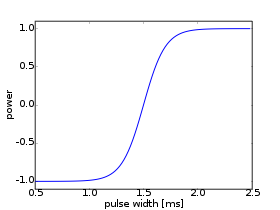Chování serva

Prvním problémem je, že max_speed není konstanta. Maximální rychlost je jiná pro každý typ serva. Je dokonce jiná pro každý kus serva. Záleží například na tom, jak je sesazené (tj. jak mu uvnitř „drhnou” kolečka) nebo na tom, zda se točí na jednu či druhou stranu. A bohužel nezáleží pouze na vlastním servu, ale i na spoustě dalších věcí, jako je například aktuální napětí na baterkách, aktuální hmotnost robota, kvalita povrchu, po kterém se robot pohybuje, jeho sklon atp. Hodnota max_speed proto vždy bude pouze a jenom poměrně hrubým odhadem.

Druhým problémem je reakce serva na šírku pulzu. Náš výpočet předpokládá lineární závislost - k krát delší pulz, k krát vyšší rychlost. Jak se ale chová typické servo je vidět na obrázku. Oblast, kde je možné rychlost serva šířkou pulzu skutečně řídit je poměrně malá. Zbytek odpovídá maximální rychlosti na jednu a druhou stranu. Navíc vždy neplatí, že nulové rychlosti odpovídá šířka pulzu 1.5 ms. I tato hodnota se může průběžně měnit.

V podstatě o všech vlastnostech serva platí to, co jsme zmiňovali o maximální rychlosti – nelze se spolehnout na to, že když jednou něco změříme, že to tak bude navždy (ať už se jedná o maximální rychlost, šírku pulzu pro nulovou rychlost či rozsah šírky pulzů využitelných k regulaci).

Řízení se zpětnou vazbou

Předpokládejme, že nelze navrhnout vztah (regulátor), který by nám z požadované rychlosti určil šířku pulzu dostatečně přesně a spolehlivě za všech podmínek. Jak můžeme docílit toho, aby se servo točilo požadovanou rychlostí? Překvapivě k tomu využijeme informaci z enkodéru, pomocí které budeme upravovat šířku pulzu a tím i výkon serva. Když bude rychlost příliš nízká, přidáme a naopak.

1. pokus

V první řadě potřebujeme znát aktuální rychlost, kterou si označíme jako cur_speed. Požadovanou rychlost označíme req_speed a rozdíl aktuální a požadované rychlosti, kterému říkáme regulační odchylka, označíme písmenkem e. Vztah pro úpravu šířky pulzu pak může vypadat třeba následovně:

e = req_speed - cur_speed
pulse_width += X * e

Tento vztah v sobě zahrnuje poměrně jednoduchou myšlenku – čím je aktuální rychlost nižší než rychlost požadovaná, tím více zvýšíme délku pulzu. V okamžiku, kdy je aktuální rychlost shodná s požadovanou, pulz dále neměníme.

Výhodou je, že ve vztahu není zahrnut předpoklad o maximální rychlosti a ani o délce pulzu odpovídající nulové rychlosti. I tento vztah však předpokládá lineární závislost, ale tentokrát pouze změny rychlosti na změně pulzu a nikoli přímo délky pulzu na rychlosti, což je požadavek o řád slabší. Navíc se díky iterativnímu charakteru, kdy se v každém kroku pokoušíme o lepší odhad šířky řídího pulzu, algoritmus lépe vypořádává se změnami ať už zmiňované lineární závislosti nebo i ostatních (vnějších) podmínek.

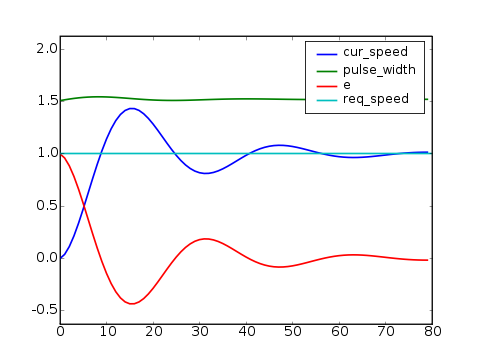1. regulátor

Simulaci, jak může vypadat chování serva při použití tohoto typu regulace, vidíte na obrázku. Servo začíná z klidu (aktuální rychlost cur_speed je nulová a pulse_width je 1.5). Požadovaná rychlost req_speed má hodnotu 1. Na obrázku je vidět jeden z poměrně častých problémů: aktuální rychlost cur_speed kolem požadované hodnoty zakmitává. V tomto případě jsou překmity způsobeny tím, že šířka pulzu odpovídá spíše aplikovanému výkonu než čemukoli jinému. Pro co nejrychlejší dosažení požadované rychlosti typicky potřebujeme vyšší výkon než potom pro její udržení. Pokud je ale odchylka kladná (požadovaná rychlost je vyšší než rychlost aktuální), tak náš jednoduchý regulátor neustále výkon přidává. My bychom ale v tomto případě potřebovali začít ubírat aplikovaný výkon dříve, než dojde k překmitu rychlosti.

2. pokus

Jak spolehlivě a jednoduše omezit překmity? V podstatě čím rychleji se blížíme k požadované rychlosti tím dříve budeme chtít začít omezovat aplikovaný výkon. Zkusíme přidat další člen, který bude reprezentovat rychlost, s jakou se aktuální rychlost mění (odhad její derivace). Pokud rychlost v minulém kroku rostla, bude přispívat ke snížení výkonu. Pokud naopak klesala, bude přispívat k jeho zvýšení.

e = req_speed - cur_speed
pulse_width += X * e - Y * (cur_speed - last_speed)

V kombinaci s regulátorem z předcházejícího kroku získáváme poměrně zajímavé chování. Dokud je první člen větší než druhý, výkon roste. Pokud je naopak větší člen druhý - tj. pokud rychlost hodně rostla, ale aktuální odchylka je malá, výkon klesá. Což je přesně to chování, co jsme potřebovali. Navíc okamžik, kdy dojde k ubírání výkonu můžeme nastavit vhodnou volbou konstant X a Y.

Na obrázku je vidět, že výsledný efekt je značný. Díky našemu tlumícímu členu bylo možné zvýšit konstantu X a tím i rychlost reakce regulátoru. Navíc jsme se zcela zbavili překmitů.

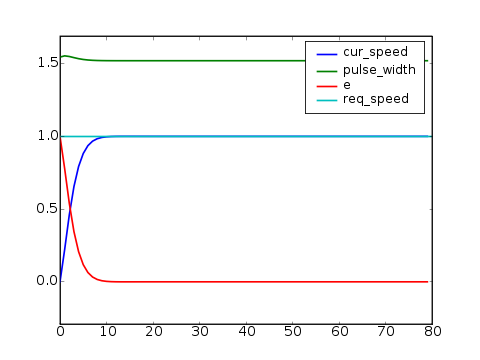2. regulátor

3. pokus

Předchozí regulátory byly formulovány jako postupné úpravy akční veličiny (akumulování změn). Toto ale není jediná možná formulace. Mohli bychom ho definovat i tak, že by akční veličinu počítal přímo? Určitě ano. Stačí rozepsat jednotlivé kroky inkrementálního regulátoru:

pulse_width = X * e_1 + X * e_2 + … + X * e_n

Získáme ale takovouto formulací něco? Určitě ano. Může se nyní lépe zamyslet nad tím, jak vlastně regulátor funguje. Vidíme, že výsledná hodnota akční veličiny vlastně odpovídá součtu všech minulých odchylek přenásobených nějakou vhodnou konstantou X. Můžeme se pak například ptát: jaká je maximální smysluplná hodnota X? Co by se stalo, kdybychom konstantu X položili rovnu hodnotě max_width/max_speed? V prvním kroku výpočtu bychom dospěli k následujícímu výsledku:

pulse_width = (max_width/max_speed) * req_speed

Tento výsledek nám může nápadně připomínat výsledek regulátoru bez zpětné vazby. Do problémů se ale typicky dostaneme hned vzápětí, protože motor většinou nereaguje hned. V následujících krocích bude aktuální rychlost stále ještě velmi malá a my bychom se akumulací takto velkých korekcí dostali velmi rychle k poměrně astronomickým hodnotám. Čím pomaleji řízený systém reaguje na změnu akční veličiny, tím větší tento problém bude. Hodnota konstanty X tedy velmi úzce souvisí s rychlostí reakce řízeného systému.

Je také důležité si uvědomit, že ke snížení výkonu dojde až v případě, kdy aktuální rychlost převýší rychlost požadovanou. To je ale právě onen překmit, který nám nevyhovuje. Bylo by možné se mu vyhnout i jinak než s využitím derivace?

Nejlepší by bylo překmitu předejít a vůbec nepřipustit, aby se výkon tolik navýšil. Jednou z cest by mohlo být zvolit hodnotu X velmi malou. Problému se ale bohužel zcela nezbavíme. Pouze ho do jisté míry omezíme. Navíc tím náš regulátor také hodně „zleniví” — bude mu dlouho trvat, než dosáhne požadované rychlosti.

Zkusme výpočet rozdělit na dvě části: první reprezentující odchylky dřívější a druhou, reprezentující odchylku aktuální:

pulse_width = X * (e_1 + e_2 + … + e_(n-1)) + Z * e_n

Toto rozdělení výpočtu nám dává možnost ovlivnit, jakou mírou se na regulaci podílí odchylky minulé a jakou odchylka aktuální, což v původní definici nebylo možné. Hodnotu X nyní můžeme zvolit dostatečně malou a hodnotu Z naopak dostatečně velkou, abychom zjistili regulátoru dostatečnou agilitu. Celý upravený výpočet pak bude vypadat takto:

e = req_speed - cur_speed
pulse_width = X * sum_e + Z * e_n
sum_e += e

V naší jednoduché simulaci je vidět, že i takto definovaný regulátor je dostatečně rychlý a přitom nepřekmitává, přičemž k tomuto chování nepotřebuje znát derivaci regulované veličiny (proč je toto značná výhoda si povíme v některém z dalších článků).

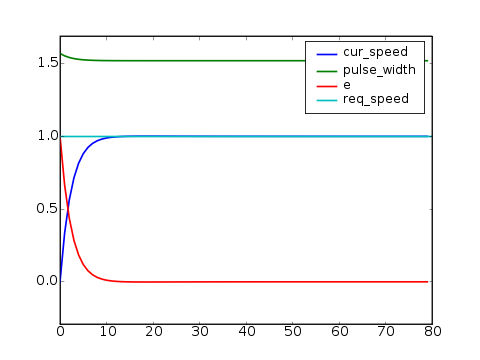3. regulátor

Formalizace zpětnovazebních regulátorů

Samozřejmě, že nejsme první, kdo se věnuje zpětnovazebním regulátorům. Proto určitě nebude na škodu, když si naše tři regulátory zasadíme do nějakého širšího kontextu. Uveďme si nejprve nejčastěji používané názvosloví:

u akční veličina
y regulovaná veličina
w požadovaná hodnota regulované veličiny
e regulační odchylka (e = w - y)

Základní tvary/typy regulátorů máme pro přehlednost v tabulce.

Typ regulátoru	Označení	Polohový (absolutní) tvar	Přírůstkový (diferenční) tvar
proporcionální	P	u_n = P e_n	Δu_n = P Δe_n
integrační	I	u_n = I ∑e_i	Δu_n = I e_n
derivační	D	u_n = D Δe_n	Δu_n = D Δ²e_n

U regulátoru, kterému říkáme proporcionální, je velikost akční veličiny přímo úměrná aktuální velikosti regulační odchylky. Tento typ regulátoru využijeme například v situaci, kdy je našim cílem natočit motor do nějaké konkrétní pozice. Regulační odchylkou je pak rozdíl v natočení a výkon motoru může být přímo úměrný této odchylce. Speciálně, nulová regulační odchylka odpovídá nulovému výkonu (nulové akční veličině).

Regulátor označovaný jako integrační se hodí naopak v situaci, kdy pro dosažení či udržení nulové regulační odchylky potřebujeme nenulovou akční veličinu. Typickou situací, kdy se využití tohoto regulátoru nevyhneme je řízení motoru takzvaně „na rychlost”, tj. když se snažíme udržet motor v určitých otáčkách. Ke vhodné hodnotě akční veličiny, která nám zajistí nulovou regulační odchylku, musíme postupně dokonvergovat.

Abych pravdu řekl, nenapadá mě případ, kde by se dal využít samostatný derivační regulátor. Pokud takový případ znáte, budu rád, když mi dáte vědět.

Rozklíčování regulátorů 1-3

První námi zmiňovaný regulátor je regulátor integrační, označovaný jako I-regulátor a to v přírůstkovém tvaru. Konstanta X se v tomto případě označuje jako I. Nevěřte nikomu, kdo vám bude tvrdit, že je to P-regulátor. K tomu nestačí jen vhodně pojmenovat konstantu . Tato chyba je poměrně častá.

Druhý regulátor je svojí definicí nejbližší proporcionálně-derivačnímu regulátoru v přírůstkovém tvaru.

Třetí regulátor je klasický PI-regulátor. Pro většinu případů je tento regulátor postačující.

Varianta „plného” PID-regulátoru se vyskytuje pouze zřídka. Vypadala by ale asi nějak takto:

e = req_speed - cur_speed
sum_e += e
pulse_width = P * e + I * sum_e - D * (cur_speed - last_speed)

Obsahuje všechny tři již dříve zmiňované složky. Jejich význam by nám teď již měl být jasný:

P tvoří základní zpětnovazební složku
I zajišťuje nenulovou akční veličinu pro nulovou regulační odchylku
D omezuje překmity

K překmitům nejčastěji dochází v případě, kdy je řízený motor slabý a reaguje na řízení pomalu (anebo máme špatně navržený regulátor). To ale není případ našeho serva a proto si ho necháme na někdy jindy.

Závěr

Regulátory se rozdělují do dvou základních kategorii: zpětnovazební a bez zpětné vazby. Nejpoužívanějším regulátorem jsou varianty PID regulátoru, který využívá k řízení zpětné vazby. Dnes jsme (mlčky) předpokládali, že máme k dispozici dokonalou informaci to tom, co řídíme. V našem případě to byla rychlost. Je ale třeba mít na paměti, že měření rychlosti je v praxi spojeno se spoustou problémů (rozlišení doma zhotoveného enkodéru může být jednou z nich). Jak se s nimi co nejlépe vyrovnat si ukážeme v jednom z dalších článků, protože je to jeden z nejdůležitějších aspektů ovlivňujících kvalitu řízení.

Související odkazy

Wikipedia

Ostatní

Komentáře a názory