Pravděpodobnostní plánování
konfigurační prostor, PRM, RRT, RDT
První přednáška z třetí, nejnáročnější, sekce se týká obecného plánování. Co dělat, když robot není konvexní a musí se otáčet? Co když se navíc už pohybuje v 3D světě? Jak řešit problémy robotů s omezeními, např. autíčko, které nemůže jet do strany? Jak plánovat pohyb animovaných postav, které mají hodně „stupňů volnosti”? atd.
Konfigurační prostor (Cspace)
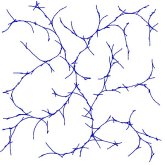 RRT pro autíčko s překážkama |
Shrneme-li to, tak konfigurační prostor je n dimenzionální prostor,
kde n je počet parametrů jednoznačně definující pozici/konfiguraci
robota.
Volný konfigurační prostor (Cfree)
Volný konfigurační prostor, je prostor všech konfigurací, které nekolidují s
žádnou překážkou. Jinými slovy jsou to všechny přípustné pozice pro robota. Aby
plánování mohlo být vůbec úspěšné, musí start i cíl náležet volnému
konfiguračnímu prostoru. Problém hledání cesty, případně sekvence dovolených
pohybů, se potom převede na hledání přípustné křivky ve volném konfiguračním
prostoru. (Mluvíme o přípustné křivce, protože na některé roboty klademe další
omezení, např. již zmiňované auto.)
Pravděpodobnostní plánovače
Popis Cfree
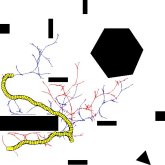 RRT pro autíčko bez překážek |
Jelikož exaktní popis Cfree je komplikovaný, pokusíme se pouze o
jeho pravděpodobnostní popis. Dále se vyhneme jeho "explicitnímu" popisu, ale
použijeme implicitní, tj. budeme mít proceduru, která nám pro danou konfiguraci
spočítá, zda patří do Cfree či nikoliv. To lze implementovat například
tak, že přímo spočítáme, zda robot v reálném (2D nebo 3D) světě s překážkou
koliduje či nikoliv.
Základní algoritmus
Algoritmus funguje ve dvou fázích, kdy nejprve vygenerujeme graf cest
(road-map) a ve druhé fázi hledáme cestu v grafu. Graf cest je
pravděpodobnostní - náhodně vybereme konfiguraci a ověříme zda náleží do
Cfree. Pokud ano, tak vytvoříme nový vrchol v grafu, a pokoušíme se
tuto konfiguraci propojit s ostatními přímou cestou. Je-li tato cesta celá v
Cfree, přidáme do grafu novou hranu. Tento proces opakujeme dokud máme
dostatek času, paměti, případně použijeme složitější test, zda již vzniklý graf
dobře popisuje Cfree.
V druhé fázi musíme nejprve napojit start a cíl. To provedeme stejným způsobem
jako náhodné konfigurace popsané v předešlém odstavci. Pak hledáme cestu v grafu.
Pokud existuje, tak máme zaručeno, že je platná - bude asi "trošku" kostrbatá,
ale s tím se dá něco dělat, viz dále. Pokud však cesta neexistuje, tak nemůžeme
nic říci - buď doopravdy neexistuje, nebo pokrytí v první fázi nebylo dostatečné.
Můžeme leda opakovat první krok a pokusit se pokrytí vylepšit…
Problém s počtem hran
Algoritmus, jak byl popsán, má zásadní problém a to s počtem hran. Pokud je
reálný prostor celkem volný, tak zbytečně vytvoříme příliš mnoho hran. Pro
neorientovaný graf, tedy graf, kdy hrana AB znamená, že se robot dostane jak z
pozice A do B, tak z B do A, lze situaci řešit pomocí grafu typu les: hranu
budeme přidávat pouze tehdy, pokud nevznikne cyklus. Počet hran tedy bude vždy
menší než počet vrcholů, ale informace o souvislosti Cfree bude
zachována.
Pokud je graf orientovaný, např. autíčko, které nesmí couvat, tak se situace
značně zesložití. Lze zabránit zbytečným lokálním cyklům, kdy vede-li cesta z A
do B, pak C, D, E, F, tak se nejprve snažíme nový vrchol X napojit na A, pak
B… a obráceně se snažíme nejprve napojit F na X, pak E, D… Končíme, jakmile se
nám to povede a další testy již neprovádíme. Globální cykly však tímto způsobem
neohlídáme.
Vyhlazování výsledné cesty
Cesta nalezená pravděpodobnostním plánovačem bývá zpravidla hodně kostrbatá.
Jednoduchý způsob, jak jí vylepšit, je pomocí náhodného převzrokování: vybereme
libovolné dvě konfigurace na cestě (nemusí to být původní "řídící"
konfigurace) a pokusíme se je přímo spojit. Pokud nová "zkratka" náleží do
Cfree, tak daný úsek nahradíme. Počet opakování vyhlazování může zase
být dán časem, konstantou nebo podmínkou na úspěšnost zkracování.
Rapidly Exploring Random Trees - RRT
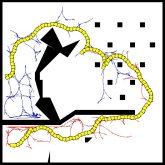 RRT pro autíčko s překážkama |
Popis algoritmu RRT
RRT, stejně jako pravděpodobnostní plánovače, používá k mapování
Cfree strom, který je však zakořeněn ve startovní pozici. Nové vzorky
jsou vždy připojovány k již existujícímu stromu, a to vždy pouze k nejbližšímu
vrcholu. Opět náhodně vybereme pozici v Cspace, ale kontrolujeme pouze
kratší cestu (krok máme zafixovaný, i když ho lze během algoritmu měnit). Pokud
je tato krátká cesta volná, tak na její konec přidáme nový vrchol. Strom se tak
rozroste pouze o malý kousek. Budeme-li tento postup dlouho opakovat, podaří
se nám rovnoměrně pokrýt prostor Cfree. Aby strom také konvergoval k
samotnému cíli, tak občas místo náhodných vzorků z Cfree vložíme přímo i
cílovou pozici. Nesmíme to dělat však příliš často, jinak by se algoritmus mohl
zaseknout v lokálním minimu.
Dvoustromová verze
Vylepšená varianta RRT generuje dva stromy - jeden ze startu a jeden z cíle.
Nově přidaný vrchol ke stromu startu se použije i k prodloužení cílového stromu
a obráceně. Tato verze má zásadní výhodu, že jak start tak cíl mají velikou
šanci se nejprve "vymotat" ze složité pozice (představte si parkování auta) a
napojení proběhne až na volnějším prostoru. Výhodné je také místo pouhého
prodloužení o pevně daný krok použít proceduru connect(), která krok opakuje
dokud to jde. Connect tak má možnost se rychleji dostat do cílové pozice.
Reference
[1] Mark H. Overmars, Petr Švestka, Motion planning for carlike
robots using a probabilistic learning approach. The International Journal of
Robotics Research, 16(2):119-143, Apr 1997.
[2] James J. Kuffner, Steven M. LaValle, RRT-Connect: An Efficient
Approach to Single-Query Path Planning Proceedings of the 2000 IEEE
International Conference on Robotics & Automation, San Francisco, CA,
p.995-1001, Apr 2000.
[3] Obrázky byly převzaty ze stránky http://msl.cs.uiuc.edu/rrt/