Scan matching
korekce odometrie, ICP a omezení
„Přišla bída na kozáky” aneb Eduro odometrie není dokonalá a je třeba s tím něco udělat. V tomto článku probereme základ matchování 2D lidarového scanu pomocí ICP (Iterative Closest Point) a jednoduché pokusy v Python + numpy.
Úvod
Matchování laserových scanu je taková „pěkná začátečnická úloha”, které jsem se leta vyhýbal,
ale teď by se mi hodila a rád bych tomu rozumněl o trošku více, co se tam děje a za jakých příležitostí
to selže. K dispozici máme teď 360 stupňové 4 úrovňové VanJee lidary a
ta vrstva vodorovným scanem je na to jak dělaná.
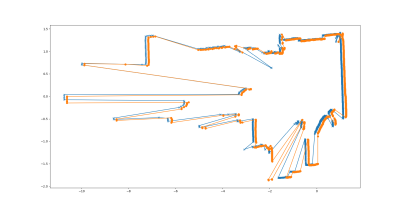
Obrázek výše je možná zavádějící, protože ukazuje 2 scany, které ale matchovat nebudeme. Je to vlastně
první předpoklad, že matchovat má smysl jen pokud 2x pozorujeme to samé prostředí (zde bod odrazu).
Pokud je podlaha vodorovná, lidar namontován vodorovně a při rozjezdu a brždění se robot příliš nekolíbá,
tak dává smysl jednotlivé scany porovnávat (zde světle zelené). Na druhou stranu scan sklopený 10 stupňů
dolu (hnědý) je pro matchování nepoužitelný — při změně pozice jsou skoro všechny body jiné.
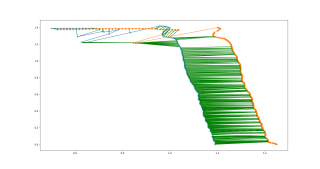
Tak teď snad vhodnější obrázek co se snažíme namatchovat:
Toto jsou dva scany cca po 1s, tj. s mírným posunem jízdou rovně. A teď co? Přiznám se, že na čtení
článku jsem neměl úplně náladu, tak jsem koukal na
skoro hodinové video.
Jako úvod mi to přišlo celkem poučné. Navíc je to v kontextu F1/10th,
což by mohla být docela pařba, ale my asi už zůstaneme u těch pomalejších robotů …
ICP (Iterative closest point) ve své základní
podobě vezme ke každému bodu prvního scanu nejbližší bod z druhého scanu a tím definuje páry korespondencí.
Aneb obejde tím základní problém a to, které body si vzájemně odpovídají. To je také hned první slabina,
resp. předpoklad ICP, že ty odpovídající si body budou relativně blízko. Je tedy rozhodně dobré
algoritmu pomoci, a pokud tušíme, jak se robot mezi jednotlivými scany zhruba pohyboval (z odometrie),
tak tím začít.
Pokud jednotlivé páry většinou vypadají, že „tam by bylo dobré druhý scan posunout”, tak je vše
vpořádku. A teď trik z youtube, který mne potěšil a vrátil do školních let. Pokud si
totiž vystačíte jen s 2D, tak pro řešení existuje uzavřená formule … prostě dosadíte čísla a je to.
Ano, není tak prostá:
Ještě tomu předcházel jeden slide, který ale asi je celkem předpověditelný, aneb jak by jste
dva scany (už páry bodů) posunuli, aby jejich součet vzdáleností byl minimální? Střední hodnota
x a y a ty dát přes sebe. Pěkná je ale ta rotace. Pokud uděláte korekci na
střední hodnotu a spočítáte matici kombinaci x1x2, x1y2, x2y1, y1y2, tak stačí
SVD (Singular value decomposition)
a rotaci dostanete (teoreticky) jak je na snímku z videa.
Na rovinu se to SVD, tak pěkně nepočítá, takže mne zase mile překvapilo numpy:
numpy.linalg.svd()
(jako já si musel zopakovat i násobení matic,
ale tím bych se tady moc nechlubil).
# compute translation and rotation
a, b, c, d = 0, 0, 0, 0
for (x1, y1), (x2, y2) in pairs:
a += (x1-xc1) * (x2-xc2)
b += (x1-xc1) * (y2-yc2)
c += (y1-yc1) * (x2-xc2)
d += (y1-yc1) * (y2-yc2)
m = np.array([a, b, c, d]).reshape(2, 2)
U, S, V = np.linalg.svd(m)
# rot = U * V.T
# rot = U * V
rot = np.matmul(U, V)
trans = np.array([xc1, yc1]) - np.matmul(rot, np.array([xc2, yc2]).T)
No a teď už jen drobný problém, že ta U * V není rotační matice … aha … není nad to si to sepsat.
Vždyť říkám, že mám i problém s násobením matic! Tak opravou za np.matmul už to jako rotační matice vypadá.
Chybí už jen dovětek, jestli se nejprve posouvá nebo rotuje (za mne „nekonečný příbeh”)? Ano, dopsal jsem si
unittesty na triviální případy, abych viděl co je převrácené nebo to nesedí.
Závěr? No nechal bych to s otevřeným koncem, protože by bylo dobré minimálně probrat point-line
variantu, možná nějaké optimalizační triky. Ale to raději až příště.
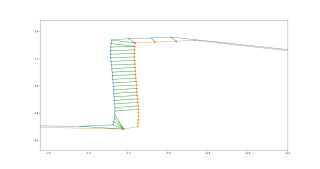
p.s. trošku jsem to poklidil, otočil směr rotace, takže i v natočení to začalo konvergovat, a výsledek vypadá takto:
 uměle otočený 2. scan o 10 stupňů |
případně python kód je zatím zde.