Bug algoritmy
hledání cesty pro jednoduché automaty
V počátcích robotiky se studovaly především problémy, jak naplánovat cestu ve zcela známém prostředí. Příkladem může být piano movers problem, tj. přestěhování klavíru do krápníkové jeskyně (3D prostředí, komplexní tvar překážek i robota). V osmdesátých letech přišel V. Lumelsky s jiným, matematicky dobře definovaným, přístupem: hledání cesty ve zcela neznámém prostředí pro automat s malou pamětí, s dotykovým senzorem a znalostí svých 2D souřadnic.
Bug1
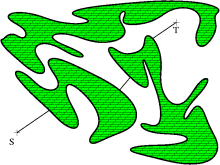 Bug1 |
- vydej se směrem k cíli
- pokud jsi v cíli KONEC - cesta nalezena
- pokud narazíš na překážku označ si tento bod H (hit point) a obcházej překážku
- monitoruj nejbližší bod k cíli (označ jej L = leave point) a ujetou vzdálenost
- po návratu do H zvol kratší cestu zpět do L
- pokud směr k cíli vede do překážky KONEC - cíl je nedosažitelný
- GOTO 1
Na tomto algoritmu si vyjasníme nutné předpoklady o robotovi a překážkách:
- Robot je pro nás pouze bod v 2D rovině. Je vybaven dotykovým senzorem a díky znalosti své pozice je schopen v každém okamžiku určit směr a vzdálenost k cíli.
- Překážky mohou být téměř libovolné. Je jich lokálně konečný počet a každá z nich má konečný obvod.
Co to znamená lokálně konečný počet? Představte si nekonečný les, ve kterém
je nekonečně stromů, ale lze jím snadno procházet. Matematicky ty znamená, že
každý kruh o konečném poloměru má průnik s konečným počtem prvků/překážek.
A jak vypadá překážka s nekonečným obvodem? Můžeme použít příklad z fraktální
geometrie — Kochovu vločku. Vločka postupně vzniká z rovnostranného
trojúhelníka, který překreslujeme. Každou úsečku nahradíme čtyřmi novými, s
tím, že každá nová úsečka má velikost 1/3 původní _/\_. Toto zjemnění provedeme
na všechny úsečky a získáme tak obvod 4/3 krát větší než původní. Opakujeme-li
tuto činnost do nekonečna, tak získáme nekonečný obvod (pro libovolně veliký
obvod O jsme schopni najít n, kdy (4/3)^n > O).
Proč máme zmíněné omezení na překážky bude jasné, pokud budeme odhadovat
maximální možnou délku cesty pomocí algoritmu Bug1:
P < D + 1.5 ∑iN pi
kde D je přímá vzdálenost start—cíl, N je počet překážek protínající
kruh se středem v cíli a poloměrem D, a pi jsou obvody
jednotlivých překážek.
Bug2
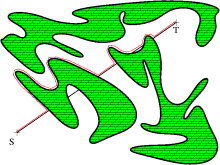 Bug2 |
- vydej se směrem k cíli
- pokud jsi v cíli KONEC - cesta nalezena
- pokud narazíš na překážku označ si tento bod H (hit point) a obcházej překážku zvoleným směrem
- pokud narazíš na úsečku start-cíl, kde je vzálenost menší než od bodu H a cíl vede směrem od překážky GOTO 1
- po návratu do H KONEC - cíl je nedosažitelný
Pokud budete pozorovat chování Bug2 jako vnější pozorovatel, tak se Vám bude
zdát inteligentnější . V čem je tedy problém? Co se může pokazit? Problémy
nastanou u složitějších překážek, které úsečla start-cíl protne mnohokrát.
Podmínka v bodě 4 musí nutně kontrolovat i vzdálenost k cíli, jinak pokud
bychom např. na obrázku k Bug2 poprvé zvolili směr vpravo a pak vždy vlevo, tak
by automat skončil v nekonečné smyčce v první zákrutě.
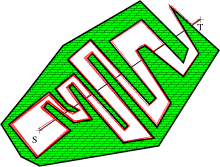 Problémová situace pro Bug2 |
P < D + 1 ⁄ 2 ∑i nipi
Bug1+2
Co si vybrat pokud máte jeden algoritmus (Bug2) ve většině případů rychlejší,
ale jsou situace, kdy dopadne hodně špatně, a druhý algoritmus (Bug1), který
sice extra rychlý není, ale dobře se vypořádá se všemi situacemi? Ideální by
byla kombinace a tak blechy zkřížíme .
Nový algoritmus Bug1+2 bude postupovat podle instrukcí Bug2 až do okamžiku
detekce problémové situace. To je případ v bodě 4, kdy objíždíme překážku a
narazíme na průsečík s úsečkou start—cíl, který je ale dále než hit point
H. Pokud k tomu dojde, tak pokračujeme v objíždění celé překážky podle
algoritmu Bug1 a bod opuštění L definujeme jako místo nejblíže k cíli. Dále
pokračujeme podle algoritmu Bug2 s tím, že pro úsečku teď místo startu
použijeme bod L.
VisBug
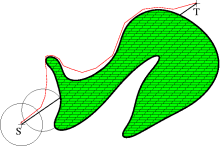 VisBug |
Další rozšíření
Bug algoritmy, jak byly popsány, předpokládají 2D prostor a statické překážky.
Další rozšíření by tedy mohlo být v odstranění těchto předpokladů.
Algoritmus Bug2 bude fungovat i v 3D prostoru, pokud např. překážky budou
konvexní. Povedeme-li řeznou rovinu danou startem, cílem a libovolným bodem,
tak i v této rovině budou překážky konvexní a algoritmus vždy najde cestu.
3D prostor je ale zrádný a tak pro složitější (skoro by se dalo říci normální)
situace ani nemusí existovat rovina, kde by se dala cesta nalézt. Lumelsky v
jednom z pozdějších článků navrhuje kombinaci Bug1 s jiným algoritmem, který
dostanete na vstupu a který umí zmapovat/objet celou překážku (pozn. v 2D tomu
odpovídalo obcházení překážky jedním směrem, dokud se automat nevrátil do zpět
výchozí pozice). Bod opuštění překážky L je opět místo nejbližší k cíli.
U pohybujících se překážek je situace matematicky nejasná. Asi nemá cenu
předpokládat jiný model než VisBug, protože jinak při objíždění hrozí srážka.
Dále je třeba vzít v úvahu rychlost překážek a rychlost našeho automatu.
Pomocí senzorů je třeba určit směr pohybu překážky atd. Jinými slovy, pokud
byste měli zájem, tak je zde jistě prostor pro bádání, ale výsledky už ztrácí
názornou jednoduchost původních bug algoritmů…
Závěr
Bug algoritmy jsou ukázkou programů pro jednoduché automaty, které znají svoji
absolutní pozici. Přestože první články vyšly před více jak dvaceti lety, stále
jsou pevným základem, na kterém mnozí další autoři dodnes staví. Bug algoritmy
jsou také dobrým příkladem jiného pohledu na složitost plánovacích úloh, která
už není popisována v číslech počtu vrcholů všech překážk a robota, ale
v odhadu nejhorší možné délky cesty.
Související odkazy
- A New Range-Sensor Based Globally Convergent Navigation Algorithm for Mobile Robots
- pěkné obrázky k tématu
- bug1, bug2
Pokud se Vám něco z toho článku přišlo špatně nebo Vám některá část přišla méně
srozumitelná, můžete se nám ozvat pomocí našeho
kontaktního formuláře.
Dodatečné poznámky
Reprezentace robota bezrozměrným bodem a následný konflikt s překážkou o
nekonečném obvodu (viz Kochova vločka) je dosti umělý. Pokud by robot měl
nenulový rozměr (např. malý kruh o velikosti eps), tak při objíždění by se
zahladily detaily komplikovaného povrchu. Potom by i délka objezdu okolo Kochovy
vločky byla konečná.