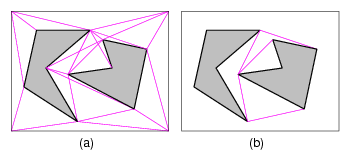
Exaktní plánování
vektorové mapy, plánování cesty ve známém prostředí
Jak najít cestu, máme-li k dispozici mapu světa? Světem se samozřejmě i tentokrát míní svět robotický, což může být např. pouze jediný pokoj s nábytkem. Mapou rozumíme seznam polygonů tvořících překážky. Zajímá nás, zda existuje cesta z aktuální pozice robota na nějaké jiné konkrétní místo, jak taková cesta vypadá, jak vypadá nejkratší cesta či jak vypadá cesta nejbezpečnější.
Mapa světa
Našeho robota na cestu do světa vybavíme lépe než v předcházejících
dílech, kde o
prostředí, ve kterém se pohybuje, nevěděl vůbec nic .
Bug algoritmy si nakonec
sice poradily s libovolným tvarem překážky, ale pokud chceme takovou
„libovolnou” překážku nějak jednoduše popsat, musíme nutně zavést
nějakou aproximaci. V tomto textu se omezíme pouze na polygony, tj. pokud
chcete popsat Váš kulatý odpadkový koš, tak místo kružnice použijete např.
dvanáctihran.
Exaktní plánování
Co je to „přesné” plánování? Jedná se o kategorii plánovacích
algoritmů, které najdou cestu vždy, pokud existuje, a v opačném případě
ověří, že neexistuje. Mohli byste si říci: „To je snad samozřejmé nebo
ne? Existují snad nějaké nepřesné algoritmy?!” Nebudu příliš
předbíhat, ale… ano existují i „méně spolehlivé” algoritmy.
Patří sem aproximační rastrové algoritmy, kdy si
zjednodušíme popis například na 10×10cm mřížku, nebo
pravděpodobnostní algoritmy, které řeší těžké problémy
s omezenou manévrovatelností robota (například model klasického auta).
Plánovací algoritmy lze rozdělit do kategorií i z jiného hlediska. Jedny se
snaží nějak popsat volný prostor pomocí rozdělení na jednoduché části –
zde si uvedeme jako příklad lichoběžníkovou dekompozici. Další algoritmy pak
vytváří mapu cest (roadmap) – sem patří např. graf viditelnosti a Voronoi
grafy. Existují i varianty kdy je svět popsán pomocí matematických klauzulí,
ale tuto variantu přeskočíme.
Algoritmy nejprve uvedeme pro robota reprezentovaného bodem (tj. jako
Bug algoritmy) a v druhém kroku je pak upravíme pro robota
tvaru kruhu případně
konvexního polygonu, který se ale nesmí otáčet. Úplně na závěr pak si pak
povíme, co dělat v případě, kdy je otáčení povoleno, a ukážeme si tzv.
algoritmus žebříku.
Lichoběžníková dekompozice
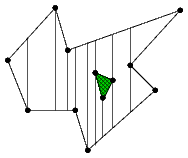 lichoběžníková dekompozice |
Pozorování: každý lichoběžník je definován právě dvěma vrcholy původních
polygonů. Trváte-li na triangulaci, pak tyto vrcholy můžete spojit (nebude tam
vadit žádná překážka) a dostanete jednodušší polygony, kterým se říká
monotónní. Polygon
je monotónní ve směru osy x, pokud jakákoli kolmice k této ose
protíná polygon nejvýše dvakrát. Takový polygon je zajímavý tím, že ho
lze již snadno triangulovat v lineárním čase – stačí postupně odřezávat
trojúhelníky ve směru monotónnosti. Navíc konvexní polygon je monotonní
vůči jakékoli přímce. Ale to jsme moc odbočili…
Svět tedy máme rozdělen na lichoběžníky, ale co to má společného s
plánováním cesty robota? Je-li robot i jeho cíl uvnitř stejného lichoběžníku,
je plánování triviální. Jednoduše lze jít přímo do cíle. Pokud tomu tak není,
je třeba nejprve nalézt seznam lichoběžníků, přes které se do cíle dostat dá. K
tomu slouží topologický graf, kde jednotlivé vrcholy odpovídají lichoběžníkům a
hrany jsou mezi lichoběžníky, které mají společnou hranu (sousedí). Robotova
cesta pak vypadá tak, že ze startu jde přímo na hranici s lichoběžníkem L2
(nechť seznam lichoběžníku je L1, L2, … Ln, kde L1 obsahuje start a Ln cíl),
odtud přímo na hranici L2 s L3, atd. Cíl se pak připojí podobně jako start s
hranicí L(n-1) a Ln.
Ok, princip je snad jasný, teď jak to naprogramovat? Je mnoho možností, z
nichž popíšeme pouze tzv. „zametání přímkou”. Budeme postupovat
zleva doprava tj. od vrcholu s nejmenší hodnotou x po největší.
Zametací přímka, někdy také označována jako koště, bude mít určitý stav –
utříděný seznam úseček podle y-ové osy, které zrovna protíná. Budeme-li
s ní postupně posouvat vpravo, uvidíme, že její stav se mění pouze ve vrcholech
původních polygonů. Tyto okamžiky, nebo přesněji souřadnice x budeme
nazývat událostmi. V případě lichoběžníkové dekompozice mohou nastat
pouze dva typy událostí: přidání a odebrání vrcholu. Aby tyto operace proběhly
rychle, používá se k implementaci koštěte vyhledávací strom (vhodným kandidátem
jsou např. červeno-černé stromy).
Celkový algoritmus pak poběží v čase O(n
log n), kde n je počet vrcholů původních polygonů.
Graf viditelnosti
Graf viditelnosti je struktura, která nám pro bodového robota umožní nalézt
nejkratší cestu mezi dvěma pozicemi. Vrcholy grafu jsou opět vrcholy původních
polygonů (překážek) plus pozice startu a cíle. Dva vrcholy jsou spojeny
hranou, pokud se vzájemně vidí, tj. pokud jejich spojnice neprochází
žádnou z překážek.
Graf viditelnosti ve skutečnosti obsahuje zbytečně mnoho hran – stačí
vzít v úvahu pouze ty, které mohou „jít za roh”. V programování to
znamená, že prodloužíte-li spojnici vrcholů, tak ani jedna strana nesmí ležet v
překážce (hranici světa také považujeme za překážku).
Je třeba si uvědomit, že graf viditelnosti může být poměrně veliký (hustý)
– představte si dlouhou chodbu s mnoha dveřmi, které musí být všechny
navzájem propojené. Rychlost algoritmu tedy závisí na počtu hran, což může být
až O(n2).
Obr v lese, Voronoi a jiné příšerky
Robot-obr už není bezrozměrný bod, ale kružnice – uznávám, že jsem Vás
asi zklamal, pokud jste čekali netvora s ručičkama a nožičkama .
Překážky (stromy) jsou body, tj. situace se nám trošku otočila. Obr se nachází
někde uvnitř lesa a má za úkol z něj utéci. Jedná se tedy zase o úlohu
plánování cesty tentokráte pro kruhového robota, kde cíl si zvolíme libovolně
daleko „od lesa” (když už obr les opustí, tak ho může snadno
obejít). Úlohu lze ještě zkomplikovat: jak moc může obr ještě přibrat, aby se
stále z lesa dostal (případně kolik musí zhubnout)?
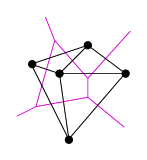 Voronoi diagram |
Každá Voronoi hrana má jistou průchodnost – vzdálenost svých
dvou řídících bodů. Konečný algoritmus tedy vypadá tak, že robot se nejprve
posune na síť Voronoi hran (to lze např. tak, že se vydá směrem pryč od
nejbližšího stromu) a pak už pouze hledáme cestu v grafu. Má-li být robot co
nejtlustší, tak z možných variant cest vždy vybíráme tu s největší
průchodností.
Co když nemáme bodové překážky, ale zase polygony? Situace je podobná, pouze
k řídícím bodům přibudou řídící úsečky a Voronoi hrany mohou být kromě úseček
kousky parabol. Chcete-li tedy najít nejbezpečnější cestu (ve smyslu
vzdálenosti od překážek), lze opět použít Voronoi diagramy.
Jak se Voronoi diagramy konstruují? Je mnoho pěkných algoritmů od zametání
přímkou, inkrementální testování kružnice až po rozděl a panuj. Pro představu
je asi nejsnazší metoda rozděl a panuj, kdy množinu překážek dělíme na menší
dokud se nedostaneme ke dvěma, kde je situace triviální (pro dva body máme dvě
oblasti rozdělené osou jejich spojnice). Ve druhém kroku pak jednotlivé
oblasti skládáme. Aby tento krok byl co nejjednodušší, snažíme se oblasti co
nejvíce oddělit – na začátku před dělením body utřídíme podle
x-ové osy a pak je rozdělíme na dvě poloviny. Spojení je potom třeba
řešit pouze na hranici.
Plánování pro konvexního robota
Voronoi diagramy už jeden případ řeší a to, když je robot reprezentován kruhem.
Ten má pro plánování zásadní výhodu, že nám nevadí, když se otáčí - prostě vypadá
pořád stejně. To ale neplatí pro ostatní konvexní oblasti, a tak se nejprve
omezíme pouze na posun a reprezentaci konvexním polygonem.
Trik, který pro plánování robota ve tvaru konvexního polygonu použijeme, je ten,
že úlohu matematicky převedeme na původní případ. Z robota tedy uděláme zase bod a
překážky nafoukneme. Je třeba si dát pozor, protože nově vzniklé překážky se mohou
protínat (dokonce některé mohou protínat i samy sebe). Na výsledné, nafouknuté,
prostředí už můžeme použít jeden ze zmiňovaných algoritmů.
Plánování s otáčením
Náznak řešení
Jak asi tušíte, není řešení úplně triviální. Nejjednodušším případem je tzv.
problém žebříku, kdy je robot reprezentován úsečkou (na obrázku je nakreslen
spíše jako špendlík s hlavičkou, která je referenčním bodem „robota”). Pro
řešení problému použijeme lichoběžníkovou dekompozici s tím, že směr rovnoběžek
volíme podle směru žebříku. Vzniklé lichoběžníky lze pak „oříznout” o délku
úsečky. Tímto některé lichoběžníky úplně zmizí, jiné se změní se v
trojúhelník. Každý lichoběžník může mít až čtyři sousedy, se kterými má společné
virtuální hrany. Ty se v této fázi, v závislosti na jejich délce, mohou stát neprůchodné.
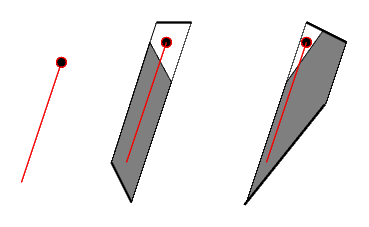 oříznuté lichoběžníky |
Ve druhém kroku zkusíme žebřík trošku naklonit. Rozklad na lichoběžníky už
nebudeme tedy dělat prodlužováním svislých paprsků, ale trošku nakloněných.
Když se podíváme na odpovídající topologický graf, tak pro malililinké
pootočení se nezmění. Tj. zůstane zachována sousednost i
průchodnost/neprůchodnost jednotlivých lichoběžníků.
Budeme-li v otáčení pokračovat, tak po jisté době ke změně přeci jenom dojde.
Tento okamžik se dá ale přesně spočítat - tj. lze zjistit, kdy lichoběžník
zanikne, stane se nepropustným, změní sousedy, případně vznikne nový. Budeme-li
tedy otáčet o 360 stupňů, dostaneme složitější graf, kde se žebříkem již můžeme
jak posouvat, tak otáčet.
Topologický graf pro otáčení
Nyní chvíli budeme ignorovat skutečnost, že žebřík má nějakou
konkrétní velikost ž a budeme se zajímat o topologický graf s otáčením.
Prořezání grafu pak provedeme až v dalším kroku.
Jak již bylo dříve naznačeno, pokud změníme směr o nějaký malý úhel, tak
topologický graf odpovídající lichoběžníkové dekompozici zůstane stejný. Je
třeba si uvědomit, že samotné lichoběžníky jsou už jiné — co zůstává
zachováno jsou jejich řídící vrcholy a strany tvořeny původními překážkami.
Budeme-li v otáčení pokračovat dále, tak se nutně v nějakém okamžiku zasekneme.
Je to případ, kdy jeden z lichoběžníků se zúží natolik, že to bude vlastně
pouze úsečka tvořena jeho dvěma řídícími vrcholy. V tomto okamžiku vytvoříme
„nové patro” topologického grafu. Okolí zanikajícího lichoběžníku L (tj.
nejvýše čtyři další lichoběžníky L1, L2, L3 a L4) zdvojíme a označíme je úhlem
pro který ke změně došlo. Ke každému uzlu topologického grafu teď odpovídá
takový zkroucený lichoběžník v 3D a pro jeho popis potřebujeme vedle
řídících vrcholů a stran původních překážek ještě limitní úhly, kdy
vznikl a kdy zanikl.
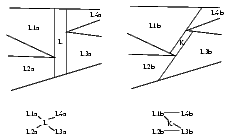 Zánik a vznik lichoběžníku |
Jak zjistit, kdy k zániku/vzniku lichoběžníku dojde? Limitní případ odpovídá
směru spojnice dvou řídicích vrcholů. Pokud již máme dekompozici pro nějaký
úhel, tak další změna nastane pro směr odpovídající nejmenšímu úhlu většímu než
je aktuální. To lze zjistit relativně rychle, tedy v čase O(E log E), kde
E je počet změn. Kolik událostí (změn) E bude nastávat? Zde je dobré si
uvědomit, že každá spojnice řídicích bodů odpovídá hraně z grafu viditelnosti,
tj. změn může být relativně hodně (O(n^2), kde n je počet vrcholů).
Prořezávání grafu
Jak je to s průchodností mezi dvěma lichoběžníky? Pokud
spolu sousedí (pozn. v nedegenerovaném případě může mít lichoběžník až čtyři
sousedy), tak sdílí společnou „virtuální” hranu (na obrázcích bez otáčení to
jsou úzké svislé úsečky). Tato společná hrana má nějakou délku l a vlastně
nám určuje jaký největší žebřík můžeme posunem touto spojnicí prostrčit.
Pokud máme žebřík nějaké konkrétní délky ž, tak budeme postupně v
topologickém grafu odstraňovat hrany, pokud je délka společného přechodu menší
než ž. Může se stát, že se žebřík vejde do nějakého lichoběžníků a přitom
předchozím procesem byly hrany ke všem jeho sousedům odstraněny? Ano, tato
varianta může nastat a je to právě případ lichoběžníku, který měl původně více
jak dva sousedy.
Při úpravě grafu ještě zkontrolujeme jednotlivé lichoběžníky, zda se do nich
vůbec žebřík v nějaké poloze (s pevnou orientací) vejde. Pokud ne, tak jemu
odpovídající uzel z topologického grafu odstraníme (s hranami si nemusíme dělat
problémy — ty byly již nutně odstraněny v předešlém kroku).
Co se děje s průchodností když postupně měníme natočení? Předpokládáme interval
úhlů, kde se jinak nemění topologie z předchozího kroku — zajímá nás pouze
kdy v daném intervalu hrana bude průchozí/neprůchozí, případně kdy je zcela
lichoběžník ořezem zanikne/vznikne.
Délku virtuální hrany lze spočítat pomocí funkce f(alfa, A,
BC)=dist(A,BC)/cos(alfa), kde alfa je úhel kolmice k přímce BC a
dist(A,BC) je vzdálenost od bodu A k přímce BC. Máme-li pevnou velikost
žebříku, tak během daného intervalu mohou dokonce nastat dvě změny
průchodnosti.
Tímto způsobem se nám topologický graf dále zjemní. Pokud původní zkroucený
3D lichoběžník byl platný v intervalu (alfa, beta), po testu průchodnosti
hran se rozdělí na podintervaly (alfa, gama1), (gama1, gama2) … (gamaN,
beta), kde úhly gama odpovídají změnám průchodnosti. V extrémním případě
lichoběžníku se čtyřmi sousedy se může interval rozpadnout až na dvanáct
podintervalů (3 případy * 4 virtuální hrany).
Realizace samotného pohybu
Jak již bylo dříve zmíněno, při otáčení směru lichoběžníkové dekompozice
dochází ke změnám tvaru lichoběžníků. Co zůstává pevné jsou řídicí vrcholy a
původní překážky. Máme-li tedy realizovat pohyb žebříku po cestě nalezené v
topologickém grafu, musíme zajistit, že robot nikdy neprotíná žádnou překážku.
Jedno z řešení je střídat otáčení kombinované s posunem (pohyb v rámci jednoho
uzlu topologického grafu, tj. zkrouceného 3D lichoběžníku) a posunem
(přechod mezi dvěma uzly pro pevný úhel natočení). Umístíme-li vždy referenční
bod robota do místa těžiště zbylé části po ořezu, máme zajištěno postupné
otáčení bez kolize.
Související odkazy
- COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS
- pěkný popis divide-and-conquer algoritmu pro konstrukci Delaunay triangulace
- Fast Polygon Triangulation based on Seidel's Algorithm
- triangulace polygonu založená na lichoběžníkové dekompozici a monotónních polygonech
- Lecture 14: Trapezoidal Decompositions
- obsahuje důkaz, že počet lichoběžníků bude 3n + 1
Emil X. — Nepochopil jsem "pozorování" o monotónních polygonech. Tak
nějak jsem měl za to, ze když lichoběžník rozdělím na poloviny úhlopříčkou, tak
mám trojúhelník a basta. O čem je tam řeč?
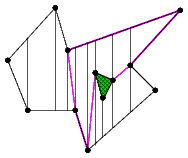 monotónní polygon |