Robotika.cz » Průvodce » Plánování na mřížce

Plánování na mřížce

Autor: Zbyněk Winkler, 2003-12-03

rastrové mapy

Dnes budeme pokračovat v plánování cesty tentokrát ovšem za použití rastrových map či pravděpodobnostních mřízek. Mnoho algoritmů zde popsaných máte příležitost potkat také v počítačové grafice. Jejich podobnost vyplývá z toho, že i na pravděpodobnostní mřížku je možné nahlížet jako na obrázek. Dozvíme se, i co je to potenciálové pole či algoritmus A*. Závěrem si ukážeme jednu z možností, jak plánovací algoritmy vhodně integrovat do řídícího systému robota.

Rastrové mapy

V minulé přednášce jsme si ukázali někteté z tzv. exaktních plánovacích algorimů. Jejich hlavní výhodou byla jejich exaktnost, neboli to, že jejich výsledkem vždy bylo přesně to, co jsme potřebovali (tj. nejkratší cesta, nejbezpečnější cesta atd). V praxi je ale třeba brát tuto jejich exaktnost s rozumnou rezervou, protože typicky narazíme na nádherný příklad GIGO principu. GIGO princip popisuje velice jednoduchou věc, která bude angličtinářům jasná již z pouhého rozepsání zkratky — Garbage In, Garbage Out (garbage = odpadky, nesmysly). Dalo by se také říci, že kvalita výsledku velmi závisí na kvalitě vstupních dat.

multimap

Vektorový popis prostředí nám umožnoval zadávat souřadnice jednotlivých vrcholů jednoduše až s přesností double, což při běžné implementaci odpovídá 8mi bytům (rozsah 1,7×10^±308). Pro srovnání – velikost atomu je možné vyjádřit v řádu 10^-10 metru. Navíc ani ty nejlepší senzory, které mohou mít mobilní roboti k dispozici, neměří s vyšší přesností než několik milimetrů (deset centimetrů je ale daleko častějším případem). Dalším faktorem ovlivňujícím kvalitu naší vektorové reprezentace je i to, že jsme se omezovali pouze na polygonální překážky a obecné překážky tedy musely být aproximovány.

Nabízí se zde tedy možnost reprezentovat prostředí pomocí mřížky, kde je každá buňka označena jako volný prostor nebo překážka. Velikost rastru nám automaticky definuje přesnost, s jakou počítáme.

Plánovací algoritmus nad mřížkou se tedy snaží najít posloupnost volných buněk, která nám definuje, kudy se má robot pohybovat.

Mřížka

Složitost exaktních plánovacích algoritmů se odvíjí zejména od počtu překážek v prostředí a od detailnosti jejich popisu. Plánování na mřížce má ale složitost dánu velikostí popisovaného prostoru a použitým rozlišením. S výhodou je možné využít i hierarchické reprezentace prostředí jak vidíme na obrázku. Cestu nejprve hledáme v úrovni nejvyšší, která má nejmenší rozlišení a její prohledání je tudíž nejrychlejší. Pokud cestu nenajdeme, můžeme vždy sestoupit o úroveň níže.

Pravěpodobnostní mřízky

Rastrové mapy se také přímo nabízejí pro reprezentaci nejistoty v příjimaném měření. Rozšíříme-li uloženou informaci v jedné buňce z hodnoty 0/1 na hodnot několik, můžeme reprezentovat jistotu s jakou je daná buňka obsazená/volná (získáme jakýsi šedotónový obrázek). Je možné vyhradit jednu hodnotu například pro hodnotu „nevím”, pokud celá mapa není dopředu známa. Takto reprezentovná mapa také umožňuje poměrně přímočarou integraci dat z několika různých senzorových systémů.

Plánování na mřížce

Jak nejlépe využít připravená data při hledání cesty? Je možné použít některé principy vyvinuté pro vektorové mapy? Jak moc se vlastně liší plánování nad mřížkou a nad vektorovou mapou? Tyto otázky se nyní pokusíme zodpovědět.

Potenciálová pole

Lokální minimum

Jednou z používaných abstrakcí pro plánování na mřížce jsou potenciálová pole. Základní myšlenka je velmi jednoduchá — každé buňce v mapě přiřadíme hodnotu, kterou ve finále použijeme pro rozhodnutí, kterým směrem se vydat. Cíli se budeme snažit přiřadit hodnotu co nejnižšší a startu naopak co nejvyšší. Při pohybu mřížkou se budeme snažit jít jakoby symbolicky „s kopce” dolů. Abychom se vyhnuli překážkám, přiřadíme jim hodnotu vyšší než kdekoli v mapě.

V nejjednodušším případě můžeme jako hodnotu buňky dosadit její eukleidovskou vzdálenosti do cíle. Po této inicializaci použijeme pro pohyb robota následující algoritmus: „Ze sousedních buněk vyber tu s nejnižšší hodnotou přesuň se do ní. Pokračuj dokud nedorazíš do cíle nebo dokud neuvízneš.”

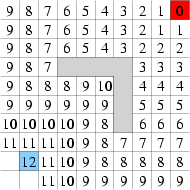Záplavové vyplňování

Algoritmus je díky své jednoduchosti a přímočarosti snadno pochopitelný i implementovatelný. Bohužel funguje pěkně pouze v případě, že prostředí obsahuje pouze konvexní překážky. V opačném případě hrozí problém uvíznutí v místě, kde potenciálová funkce tvoří lokální minimum. Lokální minimum tvoří buňka, která není cílem, a jejíž sousedé jsou buď překážky, nebo mají vyšší hodnotu potenciálu.

Náš algoritmus tedy vylepšíme. Hodnoty buňkám přiřadíme pomocí algoritmu záplavového vyplňování. V angličtině se s ním můžete také setkat pod názvy wavefront-expansion nebo flood fill. Začneme v cíli a opět mu přiřadíme hodnotu 0. Poté opakujeme následující postup: vezmi všechny neočíslované volné buňky sousedící s již očíslovanou buňkou a přiřaď jim hodnotu o jedna vyšší. Opakuj, dokud není očíslovaný i cíl nebo dokud nevyčerpáme všechny neočíslované buňky.

Tento algoritmus definuje potenciálové pole, které má pouze jedno minimum a to v hledaném cíli. Navíc určí všechny buňky, ze kterých se lze do tohoto cíle dostat. Číslo přiřazené dané buňce udává vzdálenost od cíle (počet buněk, kterými se musí projít).

Grafový přístup

Zkušenějším programátorům zajisté neunikla podobnost posledního zmiňovaného algoritmu s grafovým algoritmem procházení do šířky (anglicky breath-first search). Typická implementace procházení do šířky používá frontu pro uchování ještě nezpracovaných vrcholů. Příklad v pseudokódu:

q.insert(x_g)
while (q ≠ ∅) do
    x := q.getFirst()
    if (x == x_s)
        return SUCCESS
    forall u ∈ e(x,u)
        if (u not visited)
            Mark u as visited
            q.insert(u)
return FAILURE

Jako frontu používáme q, x_g je cílová pozice a x_s pozice startovní. Z fronty vždy vybereme prvek x a všechny vrcholy u, do kterých vede hrana a jsou nenavštívené, přidáme do fronty. Předpokládáme, že virtuální hrany existují vždy mezi sousedními vrcholy.

Tento algoritmus dělí vrcholy/buňky do tří kategorií:

nenavštívené (unvisited): ještě nemají přiřazenu vzdálenost — na počátku všechny buňky mimo x_g
mrtvé (dead): již navšívené a všichni jejich sousedi byli také zpracováni — v jistém smyslu jsou tyto buňky opravdu mrtvé, protože již nijak nepřispějí k hledání cesty
živé (alive): již navštívené, ale má ještě nenavštívené sousedy — na počátku pouze x_g — prvky fronty q

Dijkstra

Přechod z buňky do buňky nemusí vždy stát pouze jednu jednotku. V takovém případě můžeme s výhodou uplatnit Dijkstrův algortimus pro hledání nejkratší cesty v grafu. Jediná modifikace spočívá v náhradě obyčejné fronty frontou prioritní, která třídí vrcholy podle jejich vzdálenosti.

A*

Algoritmus A* je modifikací Dijkstrova algoritmu. Dijkstrův algoritmus nám našel všechny možné buňky, ze kterých se můžeme do našeho cíle dostat. Důsledkem tohoto chování je, že algoritmus prochází zbytečně mnoho buněk než najde x_s. Algoritmus A* zlepšuje dále toto chování další úpravou třídění vrcholů ve frontě. Vrcholy nejsou tříděny pouze podle jejich vzdálenosti od x_g, ale podle součtu této vzdálenosti s odhadem vzdálenosti od x_s. Pokud je tento odhad vždy odhadem spodním (tj. nikdy není vyšší než skutečná vzdálenost do x_s — můžeme použít třeba obyčejnou eukleidovskou vzdálenost), pak i tento algoritmus vždy najde cestu nejkratší. V limitním případě, kdy je odhad vzdálenosti vždy 0, algoritmus degeneruje na základní Dijkstrův algoritmus.

B*

Pokud frontu třídíme pouze podle odhadu vzdálenosti do x_s získáme ještě agresivnější algoritmus, u kterého ale již není garantováno, že nalezne opravdu cestu nejkratší. V jednoduchých prostředích ho lze ale s úspěchem využít.

Pseudo-Voronoi diagramy

Ne vždy nám vyhovuje nejkratší cesta. Někdy se například chceme držet daleko od překážek. Již známe Voronoi diagramy pro body a polygony. Je možné je definovat i nad mřížkou?

Můžem spustit procházení do šířky z každé překážky zvlášť. Voronoi hranu definujem tam, kde se nám setkají vlny ze dvou různých překážek.

Takto předzpracovanou strukturu můžeme s výhodou využít i pro opakované hledání cest. Ze startu i z cíle spustíme prohledávání do šířky a počkáme, než nám najde cestu na některou Voronoi hranu. Poté postupujeme po hranách až do části obsahující cíl, kde nám druhé prohledávání do šírky definuje zbylou část cesty.

Která cesta je nejlepší?

Zatím jsme se věnovali pouze hledání nějaké (případně nejkratší) cesty na mapě reprezentované mřížkou s hodnotami 0/1. Jak tedy do našich algoritmů začleníme fakt, že si tou mapou vlastně nejsme až tak moc jisti? Potom nám to také vzniká otázka, kterou jsme museli částečně řešit i v předcházející části — a to která cesta je vlastně ta nejlepší? Je to ta nejkratší (graf viditelnosti), nejbezpečnější (Voronoi diagramy), nejrychlejší, nejjistější (pouze přes známé volné prostředí) nebo nějaká jejich kombinace?

Potenciály podruhé

Jednou z metod jak získat cestu beroucí v úvahu výše zmiňované požadavky zároveň je alternativní definice potenciálového pole inspirovaná šířením tepla v prostředí. Cíl definujeme jako zdroj tepla (vždy má hodnotu 1), překážky pak mrazí (vždy hodnota 0). Ostatní buňky mají svoji hodnotu definovanou tak, aby stejné množství tepla přijaly i odevzdaly. Označíme-li proměnnou U(i,j) stav buňky na pozici (i,j), tak lze rovnovážný stav příjmu a výdaje popsat takto: (U(i-1, j)-U(i,j)) + (U(i+1, j)-U(i,j)) + (U(i, j-1)-U(i,j)) + (U(i, j+1)-U(i,j)) = 0. Po spočítání potenciálového pole se pak robot snaží jít směrem nejvyššího nárustu tepla.

Výpočet rovnovážného stavu odpovídá řešení soustavy rovnic, kde U(cil) = 1, U(překážka) = 0 a zmiňovaná rovnice pro všechny ostatní buňky. Problém této soustavy je, že je hodně veliká - počet rovnic odpovídá počtu buněk. Řeší se tedy pomocí numerické matematiky, konkrétně Gauss-Siedelovou metodou. Jedná se o iterační metodu, kdy postupně provádíme korekce jednotlivých proměnných: U(i,j) = ¼ (U(i-1, j) + U(i+1, j) + U(i, j-1) + U(i, j+1)).

Úlohu nyní můžeme dále rozšiřovat. Podobně jako v počítačové hře Warlords, kde se jednotlivé postavičky pohybují rychlostí v závislosti na obtížnosti terénu, můžeme i my jednotlivým buňkám přidat koeficient propustnosti. V Gauss-Siedelově metodě tedy k průměru sousedů použijeme extra koeficient M(i,j) odpovídající propustnosti: U(i,j) = M(i,j) ¼ (U(i-1, j) + U(i+1, j) + U(i, j-1) + U(i, j+1)). Pokud nechceme, aby se robot pohyboval blízko překážkám, tak zvolíme hodnotu M(i,j) pro přilehlé buňky blízké nule (0 odpovídá absolutní neprůchodnosti). Obdobně můžeme vážit dosud nezmapované části prostoru, a preferovat tak hledání cesty spíše ve známých oblastech.

Problémy

Asi hlavní problém této potenciálové metody je její pomalý výpočet. Rozhodně není real-time a nelze tedy používat k jednoduchému vyhýbání se překážkám. Na druhou stranu má metoda ale pouze jedno maximum, takže pokud cesta existuje, tak bude nalezena.

Druhý problém se týká samotných výpočtů. Dochází zde totiž k expenenciálnímu poklesu hodnot, takže i proměnná typu double stačí maximálně na 1000 kroků. To lze řešit rozšířenou aritmetikou, ale v důsledku je pak celá metoda ještě pomalejší.

Související odkazy

Motion Planning Using Potential Fields: článek na serveru GameDev.net, potenciálové pole v kontextu programování her, 2000
Interactive Motion Planning Using Hardware-Accelerated Computation of Generalized Voronoi Diagrams: jak počítat diskrétní aproximaci Voronoi diagramu pomocí grafické karty (pdf,avi), 1999
UNC Geometry Group: Video: soubor animací plánovacích algoritmů
Petr Štěpán: Vnitřní reprezentace prostředí pro autonomní roboty (disertační práce)
A* Algorithm Tutorial: přehledné vysvětlení algoritmu včetně vzorové implementace v C++, 1999
A* Pathfinding for Beginners: úvod do A* pro uplné začátečníky, včetně vzorové implementace v C++, 2003
Potential Fields Tutorial: základy (lokálních) potenciálových polí

Komentáře a názory