czech english
Robotika.cz » Průvodce » Měření rychlosti

Měření rychlosti

Autor: Zbyněk Winkler, 2005-11-10
jak se vypořádat s nepřesnými daty

Jak kvalitní je informace o rychlosti z enkodérů? Jaké má rozlišení? Toto jsou důležité otázky pro kvalitu řízení, protože jak řekl někdo chytrý: „Co neměříš, to neřídíš.” Jak tedy dostat z daných informací maximum se dozvíte právě v tomto článku.

Kvalita měření rychlosti

Základním principem fungování senzorů je jejich schopnost převádět měření různých fyzikálních vlastností či skutečností na elektrické napětí. Toto napětí je na vstupu do výpočetní jednotky převedeno na číselnou hodnotu. Posloupnost takových měření je tedy zaznamenána jako posloupnost číselných hodnot.
Každé měření jako takové je zatížené určitou chybou, protože je to vlastně pouze náš (nedokonalý) pokus o zjištění oné pravdivé hodnoty. Velikost a charakter této chyby jsou ovlivněny mnoha faktory, které nemáme, a typicky ani nemůžeme, mít pod kontrolou. Zdrojem chyb může být cokoli od vlastního senzoru až po převod napětí na číselnou hodnotu v počítači.
Pro robota je tedy velmi důležité umět všechna měření správně interpretovat. Každé další měření nám dodává novou informaci o hodnotě měřené veličiny, a proto jejich vhodnou kombinací můžeme získat jak kvalitnější odhad příslušné veličiny, tak i informaci kvalitě tohoto odhadu.

Konstantní hodnota

Nejjednodušší situace nastává, když víme, že veličina, která nás zajímá, má konstatní hodnotu (tj. s časem se nemění).

Průměr

Kombinace měření jedné veličiny pomocí průměrování asi nebude pro nikoho překvapením:
sum = 0.0;
	for (i = 0; i < n; i++)
	   sum += y[i];
	avg = sum/n;
Popsaný způsob výpočtu můžeme použít, pokud máme v jednom okamžiku k dispozici všechna měření y[i]. Často se nám ale stává, že potřebuje průměr postupně zpřesňovat tak, jak nám přibývají měření. Počítat v tomto případě celý průměr znovu by bylo neefektivní a vyžadovalo by to, abychom si pamatovali všechna doposud obdržená data.
Průměr
Průměr
Průměr můžeme počítat i postupně:
avg = (avg*(n-1) + y[n]) / n;
Tento zápis je ale ekvivalentní
avg = avg + 1/n * (y[n] - avg);
který nám názorněji popisuje výpočet průměru v kroku i, jako úpravu průměru z kroku předcházejícího určitým korekčním členem skládajícím se ze dvou částí:
  1. „váhy” (v tomto případě 1/n)
  2. rozdílu nového měření a původního průměru
Odchylka nového měření od původního průměru je tedy základem, pro získání průměru nového. Čím více měření již máme v průměru integrováno, tím menší má tato odchylka vliv (tím více našemu průměru „věříme” ve srovnání s novým měřením).
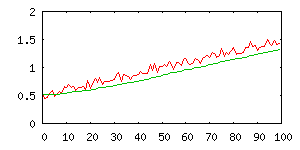
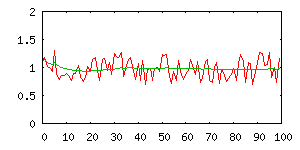
Rekurzivním výpočtem průměru jsme se sice zbavili nutnosti pamatovat si všechna doposud získaná data a můžeme postupně integrovat nová měření, ale stále odhadujeme pouze konstantní veličinu. Znázorníme-li graficky tento postup, vidíme, že se vlastně snažíme naměřenými daty proložit vodorovnou přímku.

Pomalu se měnící hodnota

Pokud se měřená veličina mění, musíme zvolit jiné řešení (proložení vodorovné přímky všemi daty by nám v tomto případě moc nepomohlo). Co můžeme udělat, je proložit onu přímku pouze několika posledními hodnotami.

Plovoucí průměr

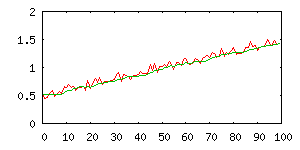Plovoucí průměr pro k=8
Plovoucí průměr pro k=8
Plovoucí průměr, je průměr z několika posledních hodnot:
sum = 0.0;
	for (i = n-k; i < n; i++)
	   sum += y[i];
	avg = sum/k;
I plovoucí průměr můžeme počítat rekurzivně a složitost výpočtu tedy nemusí záviset na délce k průměrovacího okna:
avg = (avg*k - y[n-k] + y[n]) / k;
V tomto vztahu reprezentuje člen avg*k součet posledních k měření. V dalším kroku od tohoto součtu tedy odečteme nejstarší měření x[n-k] a naopak přičteme nové měření x[n], čímž získáme součet posledních k měření. Vydělením hodnotou k tedy získáme průměr z posledních k měření.
I rekurzivní výpočet plovoucího průměru si můžeme přepsat jako součet posledního průměru a určité korekce:
avg = avg + 1/k * (y[n] - y[n-k]);
Váha určující vliv korekční složky je nyní konstantní a odpovídá převrácené hodnotě délky průměrujícího okna. Velikost korekce je dána rozdílem nejnovějšího a nejstaršího měření.
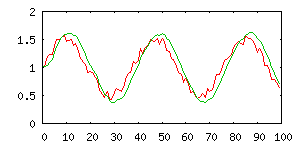
Plovoucí průměr tedy prokládá vodorovnou přímku posledními k měřeními (viz obrázek). Rekurzivní definicí výpočtu jsme opět získali konstantní složitost (tj. složitost nezávislou na délce průměrovacího okna). Stále si ale musíme pamatovat všech posledních k měření, která jsou zahrnuta do plovoucího průměru.

Odhad plovoucího průměru

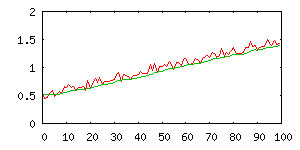Odhad plovoucího průměru pro k=8
Odhad plovoucího průměru pro k=8
Pokud si nechceme nebo nemůžeme pamatovat všechna měření z průměrovacího okna, musíme se pokusit tato data něčím nahradit, nějak je odhadnout. Nejlepší odhad nejstaršího měření, které bychom chtěli z výpočtů odstranit, je poslední hodnota průměru. Místo vlastního měření, tedy odečteme posledni průměr:
avg = (avg*k - avg + y[n]) / k;
Při zápisu pomocí korekce pak:
avg = avg + 1/k * (y[n] - avg);
Touto úpravou získáme jednoduché, rychlé a praktické řešení, které bude ve většině případů dostačující. Popisované řešení se někdy nazývá průměrování s exponenciálním zapomínáním, protože výsledná hodnota obsahuje např. i naše první měření y[0]. Jeho váha je však ((k-1)/k)^n a tedy exponenciálně klesá.

Rychle se měnící hodnota

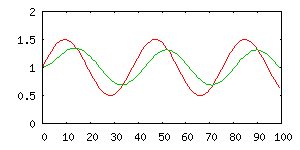
Co ale dělat v případě, kdy se měřená veličina mění rychleji než „pomalu”? Aplikace plovoucího průměru v takovém případě má ten nepříjemný důsledek, že průměrovaná hodnota jakoby plave za skutečnou s určitým zpožděním a navíc zaobluje špičky (více na obrázcích).
k=16
k=16
Sinus bez šumu, k=8
Sinus bez šumu, k=8
Toto chování je způsobeno jedním předpokladem, který je v plovoucím průměru schován – tj. že hodnota je v rámci průměrovacího okna konstantní. Pokud ale máme signál, který se v rámci průměrovacího okna výrazně mění (a tyto změny nejsou způsobeny šumem), dojde ke zmiňované degradaci (ztrátě informace).
Klíčem k řešení je použití složitějšího modelu chování a to například tak, že místo konstantní hodnoty budeme očekávat hodnotu lineárně se měnící – místo jednoho parametru budeme tedy odhadovat parametry dva, a a b (y = a*x + b).

Kalmanův filtr

Hodně zjednodušeně by se dalo říci, že Kalmanův filtr je takový „vylepšený” odhad plovoucího průměru. Toto vylepšení spočívá v rozdělení algoritmu do dvou kroků:
  • predikci nového stavu
  • korekci integrací nového měření
V případě odhadu plovoucího průměru, byla predikce stavu pro následující krok velmi jednoduchá – předpokládalo se, že se nemění .
avg = avg
Navíc budeme chtít nějakým způsobem reprezentovat „zapomenutí nejstaršího měření”. Toho dosáhneme tak, že si budeme pamatovat, jak moc našemu aktuálnímu odhadu (ne)věříme. S každou predikcí jakoby snížíme důvěryhodnost (nebo spíše zvýšíme nedůvěryhodnost) našeho odhadu:
P = P + Q
Korekci nově predikovaného stavu provedeme pomocí nového měření:
avg =  avg + K*(y[n] - avg)
kde K je určitá váha (u plovoucího průměru jsme používali převrácenou hodnotu délky průměrovacího okna). Kalmanův filtr definuje K, Kalmanovo zesílení (Kalman gain) jako:
K = P / (P + R)
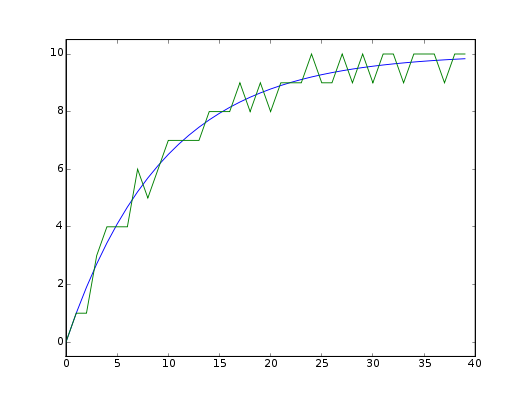
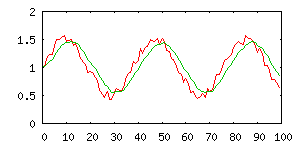1D Kalmanův filtr odpovídající k=4
1D Kalmanův filtr odpovídající k=4
kde R je míra „nedůvěryhodnosti” měření (nebo také množství šumu). Kalmanovo zesílení je vždy menší než 1, tj. „filtr filtruje” . Pokud by R bylo rovno 0, znamená to, že měření má naši 100%ní důvěru, a proto aplikujeme celou korekci. Jinak aplikujeme vždy pouze její část, která je dána poměrem nedůvěryhodnosti odhadu stavu a měření.
Po korekci vlastního stavu bychom rádi opravili i jeho aktuální míru nedůvěryhodnosti. Tato korekce je definována jako:
P = (1 - K)*P
Tento vztach lze interpretovat tak, že pokud jsme použili jednu desetinu z korekce stavu, zmenšila se nedůvěryhodnost našeho odhadu na devět desetin.
Pokud zvolíme P=0,9, Q = 0,1 a R = 9, degeneruje náš příklad na odhad plovoucího průměru pro délku okna 10.

Odvození vztahů pro Kalmanův filtr

Na příkladu jsme si ukázali, ze pro konkrétní hodnoty P, Q a R může Kalmanův filtr počítat odhad plovoucího průměru. Je to tak ale i v obecném případě?
Při výpočtu průměru jsme předpokládali, že jednotlivá měření pro nás mají stejnou váhu, a že se tedy na výsledku podílí stejnou měrou. Dále definice rekurzivního výpočtu průměru je vlastně vážený průměr dvou čísel, kde jedno má váhu n-1 a druhé 1, protože to první reprezentuje průměr n-1 hodnot. Podobně jsme uvažovali i při odhadu plovoucího průměru s tím rozdílem, že obě váhy byly konstantní k-1 a 1.
Kalmanův ale není definován pomocí vah, ale pomocí rozptylů — tedy nikoli pomocí důvěryhodnosti hodnot, ale naopak jejich nedůvěryhodnosti.
Jak by asi tak mohl vypadat vhodný převodní vztah mezi vahou a rozptylem? Zkusme se více zamyslet nad jednotlivými kroky výpočtu. První krok kalmanova filtru se zabývá predikcí stavu pro následující krok a jeho nového rozptylu. Nový rozptyl nabývá hodnoty P = P + Q. Tento krok odpovídá snížení váhy průměru z hodnoty k na hodnotu k-1. Druhý krok integruje nové měření a snižuje rozptyl podle P = (1 - K)*P, kde K = P / (P + R). V našem odhadu průměru to odpovídá opětovnému zvýšení váhy na hodnotu k. Co kdyby rozptyl byl vlastně převrácenou hodnotou naší váhy? Museli bychom ukázat, že platí:
$ 1 / (k-1) = 1 / k + Q
K = (1 / (k-1)) / (1 / (k-1) + R)
1 / k = (1 - K) * 1/(k-1) $
Postupnými úpravami první rovnice snadno nahlédneme, že Q = 1 / k*(k-1). Předpokládáme-li nadále, že R = 1, což můžeme, protože záleží pouze na poměru hodnot R a Q, a nikoli na jejich absolutní hodnotě, získáme zjednodušením rovnice druhé vztah K = 1 / k . Dosazením do rovnice třetí ověříme, že náš původní předpoklad o rovnosti rozptylu a převrácené hodnoty váhy, byl pravdivý.

Více dimenzí

Obená definice Kalmanova lineárního filtru pro více dimenzí vypadá takto:
predikce
x–k+1 = Axk
P –k+1 = Pk + Q
korekce
xk+1 = x– k+1 + Kk+1(zk+1 – Hx– k+1)
Kk+1 = P– k+1HT(HP– k+1HT + R)-1
Pk+1 = (I - KkH)P– k+1
Přestože se tento maticový zápis může zdát na první pohled dosti neprůhledný, princip zůstává stále stejný, jako při odhadu plovoucího průměru.
2D Kalmanův filtr odpovídající cca. k=4
2D Kalmanův filtr odpovídající cca. k=4
3D Kalmanův filtr
3D Kalmanův filtr

Závěr

V této kapitole jsme si ukázali, jak se vypořádat se šumem v naměřených datech ze senzorů. Viděli jsme, jak se situace komplikuje, pokud se signál rychle mění. Nakonec jsme zmínili i v praxi často používaný Kalmanův filtr. Jeho více-dimenzionální (maticovou) podobu jsme zatím pouze nastínili, protože se jedná o komplikovanější úlohu, ke které se chystáme vrátit v některém s pozdějších kapitol (stejně tak zde chybí Rozšířený Kalmanův filtr (EKF – Extended Kalman Filter), kdy model nebo měření nelze popsat lineárními rovnicemi).

Související odkazy