Robotika.cz » Průvodce » Lokalizace

Lokalizace

Autor: Zbyněk Winkler, 2003-11-03

Kalmanův filtr, MCL

Sledovnání pozice pomocí jednoduchého akumulování informací o její relativní změně časem vede k tomu, že si robot myslí, že se nachází jinde než ve skutečnosti. Důvodem je akumulace chyby, která není ničím korigována. Jak se s těmito problémy úspěšně vypořádat, se dozvíte v této kapitole.

Pro zajištění spolehlivé navigace je vhodné, aby robot věděl, kde se nachází. Proto je odhad pozice na základě informací ze senzorů jeden ze fundamentálních problémů mobilní robotiky. Tento problém může být dále rozdělen na dva podproblémy:

odhad globální pozice: schopnost zjistit pozici robota ve známé mapě
sledování pozice: průběžná aktualizace původně známé pozice

Jak jsme si minule vysvětlili, sledování pozice pouhou akumulací nejistých informací o její změně, k cíli nevede. Je tedy třeba využít informace absolutního charakteru, které nám umožní omezit nekontrolovaný nárůst chyby odhadu. Abychom to mohli udělat, je třeba nějak vhodně podchytit, co vlastně víme, co nevíme, a jak moc jsme si jisti tím, co víme .

Reprezentace chyby

Pravděpodobnostní model měření

Jednou z možností je každému měření přiřadit očekávanou chybu. Naměřenou vzdálenost potom uvádíme jako d ± r a očekáváme, že chyba má gaussovskou distribuci se střední hodnotou 0 a rozptylem r (jak je naznačeno na obrázku). Na základě takto reprezentovaných měřeních se budeme snažit zkonstruovat odhad nám neznámého stavu robota (nejčastěji x, y, úhel) a chybu tohoto odhadu.

Řekněme si pro jednoduchost, že stav robota je reprezentován pouze jedním číslem (vzdáleností na ose x). Informace z enkodérů či akceleromerů odpovídají informaci o posunu na této ose vlevo či vpravo. Jaký vliv na náš odhad pozice bude mít zahrnutí dvou informací o posunu vpravo vidíte na obrázku. Jednoduchý náhled na znázorněnou situaci nám říká, že když nevíme přesně, kde se nacházíme, a máme informaci pouze o posunu v před (také nepřesnou), tak se nám nepřesnosti kombinují a náš nový odhad je ještě nepřesnější.

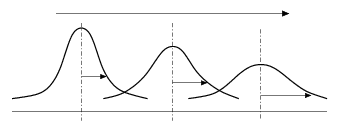Akumulace chyby

Vše možná bude jasnější na příkladu ze života. Jak přesně dokážete odhadnout jeden metr? Většina z nás to asi zvládne relativně dobře. Jak dobře potom zvládnete odhadnout 100 metrů? Tj. 100 × 1 metr? Je velmi pravděpodobné, že bez nějaké vnější reference (tj. známého okolního prostředí – stačí chodit s páskou na očích) dokonce každý z vašich pokusů dopadne úplně jinak v závislosti na tom, jak dobře se vám bude dařit odhadnout vzdálenost jednoho metru.

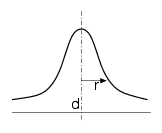
Pokud bychom tento pokus (odhad 100 metrů) zopakovali vícekrát a výsledek si zobrazili v grafu, kde osa x odpovídá skutečné vzdálenosti a osa y počtu, kolikrát jsme tuto informaci naměřili (tj. vytvoříme histogram), bude jeho tvar připomínat obrázek první, kde střední hodnota d by měla být blízko 100 metrů (vzdálenost od hodnoty 100 metrů nám říká, jak dobrý máte odhad 1 metru) a rozptyl r nám říká, jak moc se vám tento odhad v průběhu pokusu měnil.

Využití globálních informací

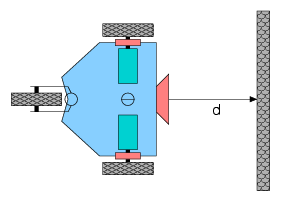Měření vzdálenosti

Chození s černou páskou na očích asi není každodenní zábava většiny z nás. A když se ani my, lidé, nezvládneme takto orientovat, tak k tomu asi težko donutíme naše roboty. Jak se tedy vlastně my, lidé, orientujeme v prostředí?

Typicky nás nezajímá vzdálenost, kterou jsme urazili na milimetr přesně a ani všechny směry, kterými jsme se kdy pohybovali. Co nás ale zajímá je, kde se nacházíme relativně vůči našemu okolí. Například když jdeme do obchodu, zajímá nás, že jsme v obchodě a nikoli že jsme urazili 22,345 m rovně vpřed, pak se otočili o 19° atd.

To, že se nacházíme na požadovaném místě, zjistíme porovnámím aktuálních vjemů s informacemi, které si pamatujeme. Jinými slovy porovnáním aktuálních údajů ze senzorů se zapamatovanou mapou prostředí.

V našem jednodimenzionálním příkladu z předcházející kapitoly to odpovídá zjištění například vzdálenosti ke stěně sonarem, či laserem. Příklad vidíte opět na obrázku. Zahrnutím měření tohoto druhu do našeho odhadu pozice můžeme dosáhnout korekce akumulované chyby. Některé konkrétní způsoby jak toho dosáhnout si vysvětlíme v následujících kapitolách.

Kalmanův filtr

Jeden ze způsobů, jak implementovat výše popsaný systém, nám poskytuje Kalmanův filtr (zmiňovaný v kapitole Filtrování dat). Zahrnutí informací relativního charakteru odpovídá predikčnímu kroku, zahrnutí absolutních měření naopak kroku korekčnímu.

Pouze je třeba, aby byly splněny určité předpoklady, které plynou z charakteru výpočtů probíhajících „uvniř” filtru. Filtr předpokládá, že pravděpodobnostní hustota reprezentující neurčitost stavu může být charakterizována střední hodnotou a rozptylem. Stejný předpoklad je kladen i na uvažovaná měření.

Proč je třeba, aby stav i měření bylo možno reprezentovat střední hodnotou a rozptylem? Zjednodušeně řečeno, Kalmanův filtr při korekci pomocí absolutních měření vnitřní stav aktualizuje vlastně jako vážený průměr stavu původního a nově změřeného. Váhy pro tento krok jsou právě převrácené hodnoty rozptylů obou těchto hodnot. Výsledný stav po korekci se tedy nachází někde na spojnici stavu původního a nově změřeného (stav se jakoby „sklouzne” směrem k naměřené hodnotě).

Pokud bychom chtěli využít měření, které tento požadavek nesplňuje, Kalmanův filtr použít nemůžeme. Bohužel taková situace může nastat snáze, než by se na první pohled mohlo zdát. Stačí uvažovat robota pohybujícího se na šachovnicové ploše se senzorem pro barvu podložky pod robotem, jako na několika nedávných ročnících soutěže eurobot (2003, 2004, 2005). Měření barvy podlahy nám neposkytuje onen jednoznačný směr, kterým bychom náš odhad stavu měli posunout. Jsme schopni pouze ověřit, zda barva podlahy v námi odhadnutém stavu se shoduje s barvou naměřenou senzory. Pokud se neshoduje, víme, že bychom měli náš stav korigovat. Bohužel nevíme, kterým směrem, protože vhodně zbarvená podlaha je dostupná všemi směry.

Monte Carlo Lokalizace

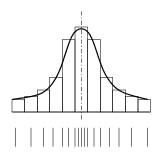Odhad distribuční funkce

Monte Carlo Lokalizace, MCL, je jiný způsob jak kombinovat nepřesná relativní a absolutní měření za účelem odhadu pozice robota. Chrakteristickou vlastností této metody je způsob reprezentace hustoty pravděpodobnosti popisující odhad pozice robota. Oproti střední hodnotě a rozptylu používané Kalmanovým filtrem, využívá tato metoda množinu tzv. vzorků. Jejich váhy a rozložení ve stavovém prostoru určuje, jak je která pozice pravděpodobná.

Výhodou reprezentace pomocí vzorků je zejména to, že neklademe žádná omezení na tvar hustoty pravděpodobnosti a jsme tedy bez problémů schopni reprezentovat i multimodální hustoty pravděpodobnosti, tedy takové, které mají více než jeden vrchol (nejpravděpodobnější pozici).

Algoritmus

Vlastní algoritmus MCL má dvě základní fáze:

predikce: posun všech vzorků na základě informací o změně pozice robota např. z odometrie
korekce: úprava vah jednotlivých vzorků na základě shody či neshody naměřených dat s očekáváními, která by odpovídala pozici reprezentované příslušným vzorkem

Výsledkem predikce je nová sada vzorků reprezentujících upravenou hustotu pravděpodobnosti na základě informací o změně pozice. Využití těchto informací by mohlo spočívat v prostém posunu každého vzorku o příslušnou hodnotu. Výsledkem by byla v podstatě totožná hustota pravděpodobnosti jako ta výchozí, pouze příslušně posunutá.

Nicméně, takto by situace vypadala pouze v případě, že bychom si informací o změně pozice byli stoprocentně jisti. V situaci, kdy i tato informace je svým způsobem nejistá, potřebujeme toto zohlednit. Potřebujeme tedy nějaký ekvivalent sčítání rozptylů, ovšem pro reprezentaci hustoty pravděpodobnosti pomocí vzorků. Toho docílíme tak, že neposuneme všechny vzorky o stejnou hodnotu. Ke každému z posunů přidáme navíc nějaký náhodný šum, jehož míra bude odpovídat míře nedůvěry, kterou k této informaci chováme. Tím získáme hustotu pravděpodobnosti, která bude svým způsobem trošku rovnoměrnější či rozplizlejší.

V této fázi chceme aplikovat krok korekce. Tento krok spočívá v modifikaci vah jednotlivých vzorků. Každý vzorek ohodnotíme podle toho, jak získané měření odpovídá předpokladu pro příslušnou pozici hodnoceného vzorku. Pokud chceme například využít informaci o barvě podlahy pod robotem, zvýšíme váhu všem takovým vzorkům, které se v mapě nachází na pozici, kde je pod robotem barva shodná s barvou naměřenou senzory a naopak snížíme, kde se neshoduje.

Tyto fáze opakujeme pro každé měření, které chceme využít k odhadu pozice. Neustálým opakováním korekčního kroku, ale časem dojde k určité degeneraci naší množiny vzorků. Většina vzorků bude mít zanedbatelné váhy a několik málo naopak váhy obrovské. Toto rozložení vah není optimální z hlediska rozložení výpočetní síly. Vzorky s malou vahou odpovídají pozicím, kde se robot pravděpodobně nevyskytuje, a proto je zbytečné se jimi zabývat. Naopak pozice s vzorky s vysokou vahou jsou více pravděpodobné, a proto bychom tam chtěli soustředit většinu pozornosti. Proto se často využívá ještě fáze třetí – převzorkování, anglicky resampling. Účelem převzorkování je v podstatě „zahodit” vzorky s hodně malou vahou a vzorky s vahou velkou naopak rozdělit na vzorků několik. Je vhodné, aby se hustota pravděpodobnosti tímto krokem změnila co nejméně, protože se na převzorkování můžeme dívat pouze jako na „implementační detail”, který do celého výpočtu jen vnáší určitý šum.

Vzorovou implementaci MCL naleznete ve zde přiložených zdrojových textech:

Makefile, point.h, frame.h, cmp.h, frame-io.h, rnd.h: podpůrné soubory
mcl.cpp: vlastní implementace MCL pro simulovaného robota
mcl.py: vizualizace vygenerovaného logu (zobrazuje vždy aktuální množinu vzorků)

Související odkazy

Particle Filters in Action: Obsáhlé stránky o částicových filtrech a jejich aplikacích zejména v mobilní robotice a zpracování obrazu. Autor Dieter Fox je jedním z původních autorů Monte Carlo Lokalizace.
Where am I?: J. Borenstein, H. R. Everett, and L. Feng, A. K. Peters, Ltd., Wellesley, MA, 1996. Systémy a metody určování polohy mobilních robotů. Obsáhlá a přehledná kniha dostupná v elektronické podobě.
The Kalman Filter: Rozcestník věnovaný Kalmanovu filtru. Tutoriály, reference, software i aktuální výzkum.
Robot Localization and Kalman Filters: Diplomová práce obsahující přehledný úvod do problematiky pravděpodobnostního určování polohy mobilních robotů.

Komentáře a názory